$P\mathop {=}\limits^{?} NP$
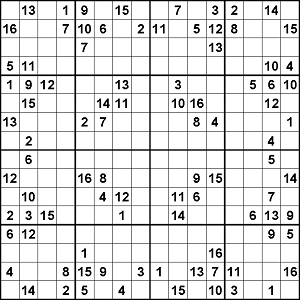
Sudoku by Philipp HübnerAbstract
Das P vs NP Problem ist eines der Millennium-Probleme, eine im Jahr 2000 erstellte Liste ungelöster Probleme der Mathematik. Das Problem ist in der Komplexitätstheorie der theoretischen Informatik verortet und bezeichnet die Frage ob ob alle NP Probleme gleich P Probleme sind, und wir müssen nur weiter suchen um einen Beweis hierfür zu finden?
Millennium-Probleme
- Im Jahr 2000 erstellter Liste ungelöster Probleme der Mathematik
- Für die Lösung eines dieser Probleme wird ein Preisgeld gewährt.
- Millennium-Probleme
- Beweis der Poincaré-Vermutung in der Topologie (solved)
- Beweis der Vermutung von Birch und Swinnerton-Dyer aus der Zahlentheorie
- Beweis der Vermutung von Hodge aus der algebraischen Geometrie
- Analyse von Existenz und Regularität von Lösungen des Anfangswertproblems der dreidimensionalen inkompressiblen Navier-Stokes-Gleichungen.
- Lösung des P-NP-Problems der Informatik
- Beweis der Riemannschen Vermutung der Zahlentheorie
- Erforschung der Gleichungen von Yang-Mills
P vs NP Problem
Problem der Komplexitätstheorie in der theoretischen Informatik12.
P – Menge aller Probleme:
- „schnell“ lösbar sind
NP – Menge aller Probleme:
- gefundene Lösung kann „schnell“ überprüft werden
- Lösungsfindung allerdings „langsam“
„schnell“ lösbar bzw. eine Lösung als „schnell“ prüfbar (siehe [comparison])
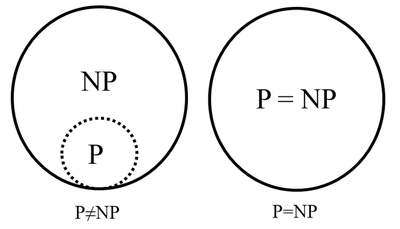
- Anstieg des Rechenaufwands wird durch mit (Polynomfunktion) beschränkt
- „langsam“: Anstieg durch (Exponentialfunktion) beschränkt
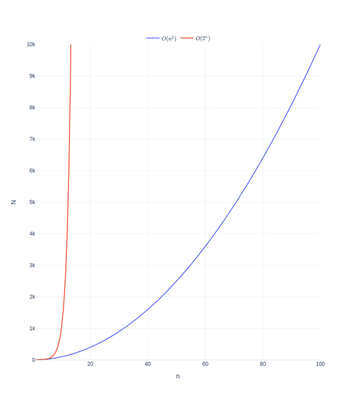
Menge P wird als Teilmenge von NP gesehen
Viele NP Probleme im Laufe der Zeit zu P Problemen geworden -> effizientere Algorithmen / Lösungsstrategien gefunden
Sind alle NP Probleme = P Probleme und wir müssen nur weiter suchen?
| P = polynomiell Laufzeit |
| NP = nichtdeterministische polynomiell Laufzeit |
P vs NP Problem
- Viele reale Probleme in NP (traveling salesman, bin packing, …)
- Ein Beweis könnte fundamentale Auswirkungen haben
- Manche glauben aber auch sehr geringe Auswirkungen da keine „direkten“ Auswirkungen
| P = NP | P != NP |
|---|---|
| - Kryptographie wäre auf den Kopf gestellt -> Sicherheitstechnische Konsequenzen (Online Banking, Kreditkartenkäufe, …) | - Meistens angenommen, da in Jahrzehnten keine „schnellen“ Algorithmen für viele NP-Probleme gefunden wurden -> Schwaches Argument |
| - Travelling Salesmann könnte „schnell“ gelöst werden -> Logistische Konsequenzen | - Fermat‘s Theorem: 358 Jahre für den Beweis |
| - Protein Struktur Vorhersagen -> Medizinische Konsequenzen | Gewissheit dass manche Dinge „schwerer“ zu lösen sind |
| Es existiert ein Unterschied zwischen Lösungsfindung und überprüfen der Lösung |
Beispiel: Sudoku
Sudokus sind NP-Harte Probleme, “einfach” zu verifizieren, aber “langsam” lösbar mit steigender Problemgröße.
Beispielsweise, in aufsteigender Komplexität3:
2x2 Sudoku
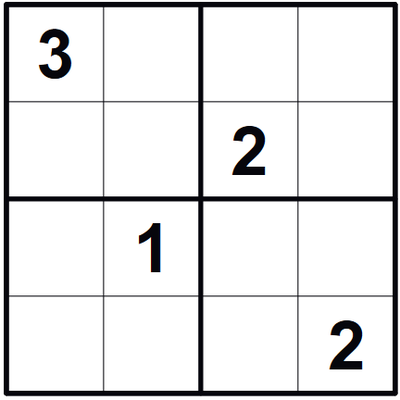
3x3 Sudoku
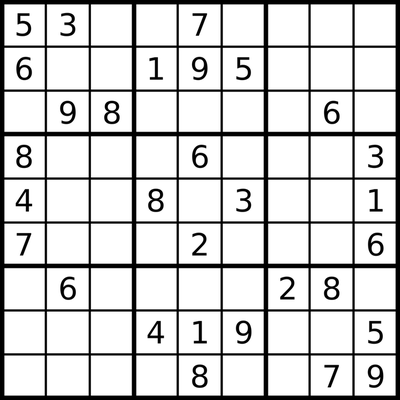
4x4 Sudoku
Marcel Albus, PhD
Senior Automation Engineer
Automation Engineer and Scientist specializing in automated pharmaceutical laboratories, industrial automation, and robotics. With expertise in mathematical optimization, machine learning, and global automation engineering, backed by a PhD from University of Stuttgart and a strong background in software development and robotic assembly systems.