Ausgangssituation

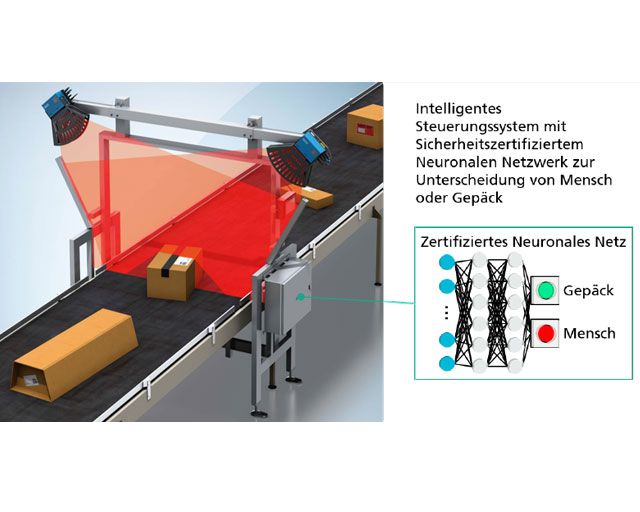
Der Check-in Bereich für Gepäck bei einem Flughafen wird allgemein in eine »Land Side« und eine »Air Side« unterteilt, wobei erstere für die Öffentlichkeit zugänglich ist. Auf dieser Seite befindet sich das Flughafenpersonal und wiegt das Gepäck, übergibt den Passagieren die Bordkarten und checkt die Gepäckstücke ein. Anschließend fährt ein Förderband die Gepäckstücke auf die »Air Side«, welche öffentlich nicht zugänglich ist und mithilfe von Sicherheitsmaßnahmen gegenüber unbefugtem oder fälschlichem Betreten gesichert ist. Die »Air Side« besitzt eine autonome Gepäckverteilung in die unterschiedlichen Flughafenbereiche, um den reibungslosen Ablauf des Flugverkehrs sicherzustellen. Die verschiedenen, höhenverstellbaren Förderbänder können bei Unachtsamkeit erhebliche Quetschungen oder andere körperliche Schäden verursachen, deshalb muss dieser Bereich sicherheitsüberwacht sein. Diese Sicherheit wird meist mithilfe von Laserscannern im Bereich der Gepäckaufgabe gewährleistet, welche den hinteren Bereich schützen und nur bei Freigabe durch das Flughafenpersonal freigeschaltet sind.

Lösungsidee

Im Verlauf dieses Exploring Projects soll der zuvor beschriebene Anwendungsfall in einer vereinfachten Version untersucht werden. Die vereinfachte Version besteht aus einem Förderband mit zwei Laserscannern links und rechts oberhalb des Förderbandes, welche die sicherheitskritische Abschaltung des Förderbands gewährleisten, falls eine Person auf dem Förderband detektiert wird. Ein Neuronales Netz (NN) soll der Steuerung hinzugeschaltet werden, welches Objekte auf dem Förderband anhand der Laserscanner-Daten entweder als Mensch oder nicht als Mensch klassifiziert (binäre Klassifikation) und als Resultat die sicherheitskritische Abschaltung im Falle einer Person auf dem Förderband gewährleistet.

Vor der industriellen Marktreife einer solchen neuen Technologie ist es nötig darzustellen, dass die Anwendung der Technologie sicher ist. Standards sind ein Mittel, um begründetes Vertrauen in die Sicherheit einer Anwendung zu schaffen. Ein anderes Mittel sind Assurance Cases, welche mithilfe von Metriken und Nachweisen eine Argumentationsstruktur aufbauen. Eine allgemein akzeptierte Argumentationsstruktur für eine solche Nachweisführung im Bereich der Künstlichen Intelligenz existiert aktuell noch nicht. Ebenso kann ein akzeptables Restrisiko für den Einsatz von Methoden der Künstlichen Intelligenz (z.B. Deep Neural Networks, Bayesian Networks) aktuell noch nicht nachgewiesen werden, was den Einsatz dieser vielversprechenden Methoden in der Sicherheitstechnik hemmt oder gar komplett blockiert.

In einem vorangegangenen Quick Check wurde die Beweisführungsmethode der Goal Structuring Notation (GSN) für solche Assurance Cases überarbeitet und für ihre Eignung im stationären Bereich angepasst sowie um neue Zusammenhänge erweitert. Hierfür wurde die GSN in drei Kategorien unterteilt: Zum einen die Reduktion von Risiken durch fehlende Spezifikationen, die Reduktion von semantischen Lücken sowie die Minimierung von Risiken durch eine deduktive Lücke. Der Fokus lag hierbei auf dieser letzten Kategorie, die Minimierung der deduktiven Lücke, wobei die Extraktion von Methoden und Metriken das Ziel war. Die identifizierten unterstützenden Methoden für eine solche Argumentationsstruktur wurden abschließend hinsichtlich ihrer Eignung bewertet. Eine identifizierte Methode ist die formale Verifikation mittels mathematischer Methoden. Die hierdurch gewonnenen Garantien bzw. Beweise würden der Argumentation eine mathematische Beweisführung beilegen, welche als starke Evidenz angesehen wird. Deshalb sollen im Verlauf des Exploring Projects die formalen Methoden im Bereich des Maschinellen Lernens untersucht, implementiert und ausgewertet werden hinsichtlich möglicher Garantien oder Beweise für einen Assurance Case. Dieser Assurance Case soll im Anschluss gemeinsam mit der University of York und der Firma SICK ausgearbeitet werden.

Nutzen

Die Ergebnisse dieses Projektes ermöglichen einen weiteren Schritt in Richtung der Verwertbarkeit von Neuronalen Netzen in sicherheitskritischen Anwendungen. Die Argumentationsstruktur könnte einen Grundstein für den Einsatz von Methoden der Künstlichen Intelligenz im Rahmen von sicherheitskritischen Anwendungen legen, wodurch sowohl neue Anwendungen erschlossen als auch bestehende optimiert werden können.

Im Sinne einer Argumentationsstruktur kann eine solche Herangehensweise in beliebigen Projekten wiederverwendet werden. Zusätzlich bringen die entwickelten Methoden zur Erzeugung von Beweisen über Qualitätsattribute von Komponenten der KI einen beachtlichen Mehrwert bei der Qualitätssicherung von KI-Methoden.

Umsetzung der KI-Applikation

Das Neuronale Netzwerk zur Erkennung von Menschen auf einer Förderband-Anwendung wurde von SICK bereits in Simulation entwickelt und steht für die Verifikation zur Verfügung. Nach eingehender Recherche der Methoden und Algorithmen für die formale Verifikation wurden mehrere vielversprechende Frameworks ausgewählt und hinsichtlich ihrer Eignung für den Anwendungsfall untersucht. Die erste Untersuchung sollte anhand eines einfachen Datensatzes aus zweidimensionalen Punktewolken stattfinden. Dieser Datensatz wurde mithilfe der bitweisen exklusiven ODER-Verknüpfung in $True$ oder $False$ im Bereich -1 bis 1 (x- und y-Achse) unterteilt. Das resultierende Bild waren vier Segmente, die abwechselnd in $True$ (1. Quadrant im Uhrzeigersinn), $False$ (2. Quadrant), $True$ (3. Quadrant) und $False$ (4. Quadrant) unterteilt wurden. Basierend auf diesem Datensatz wurde ein Neuronales Netz mit einem hidden Layer und mehreren Neuronen trainiert, welche die ReLU-Aktivierungsfunktion nutzen. Das Netzwerk sollte den Datenpunkt mit $[x, y]$ Koordinaten als Eingangspunkt in $[True, False]$ klassifizieren. Die Grenzen für die Klassifikation wurden hierbei mithilfe der Quadranten und 10% Toleranz im Vorfeld mathematisch festgelegt (bspw. für $x=[0.1 …1.0]$ und $y=[0.1 … 1.0]$ sollte die Klassifikation den Wert $True$ ausgeben). Mithilfe der vorausgewählten Frameworks zur formalen Verifikation wurde diese mathematisch festgelegte Grenze am Netzwerk überprüft. Mit anderen Worten: das Netz sollte im Bereich $x=[0.1 … 1.0]$ und $y=[0.1 … 1.0]$ immer $True$ ausgeben, was mithilfe der formalen Verifikation überprüft wurde. Nach erfolgreichem Training konnte durch die formale Verifikation mathematisch sicher nachgewiesen werden, dass das Neuronale Netz im oben genannten Bereich mit Sicherheit $True$ klassifiziert. Als Gegenprobe wurden fehlerhafte Daten im 1. Quadranten eingebracht und das Netzwerk nochmals trainiert. Nicht alle Daten im 1. Quadranten sollten als $True$ klassifiziert werden, sondern in den Daten war ein »Loch« vorhanden im Bereich $x=[0.2 … 0.4]$ und $y=[0.2 … 0.4]$. Das Netzwerk hat auch diesen Datensatz erfolgreich gelernt und konnte mithilfe der Frameworks auf die Klassifikationssicherheit überprüft werden. Die Frameworks zur formalen Verifikation konnten das »Klassifikations-Loch« im Datensatz erfolgreich erkennen und somit die Unsicherheit des Netzwerks detektieren.Dieser erste Vergleich der Frameworks hat tiefere Einblicke in die vorhandenen Implementierungen der formalen Verifikation im Bereich des Maschinellen Lernens geliefert, unter anderem wurde offensichtlich, dass die Frameworks nur sehr spezielle und einfache Netzwerkarchitekturen für die formale Verifikation unterstützen. Es können keine Convolutional Neural Networks (CNNs) überprüft werden, ebenso wenig können andere Aktivierungsfunktionen als ReLU oder Linear verwendet werden, was viele Applikationen des Maschinellen Lernens als potentielle Anwendungsfälle ausschließt, da hier die vorgenannten Kriterien nicht zutreffen. Ebenso konnte die bereits vorhandene Netzwerkarchitektur für den Anwendungsfall »Förderband« nicht untersucht werden, weshalb eine Neuentwicklung notwendig war, welche die Anforderungen des Frameworks zur formalen Verifikation erfüllt. Dieses neue Netz erreichte eine marginal schlechtere Genauigkeit als das bereits vorhandene Original-Netzwerk. Dies ist für den Prozess der formalen Verifikation nicht weiter von Bedeutung, da die Verifikation im Vordergrund steht und diese auch mit schlechterer Genauigkeit möglich ist. Für den weiteren Verlauf des Projekts wurde mit dem neuen Netzwerk gearbeitet. Von den vorhandenen Frameworks wurde das Marabou Framework ausgewählt, aufgrund seiner mathematischen Korrektheit und Vollständigkeit (es werden keine Vereinfachungen getroffen) und aufgrund seiner nativen Anbindung an die Programmiersprache Python. Marabou nutzt für die Verifikation einen Satisfiability Modulo Theorie (SMT) Ansatz, welcher ein Entscheidungsproblem als mathematische Ungleichungen formuliert, gegen welche das Netzwerk getestet wird. Ein Problem hierbei ist die Definition der Ungleichungen als Attribute. Bei dem beschriebenen Laserscanner-Anwendungsfall muss jeder Laserstrahl der Laserscanner, der an der endgültigen Klassifikationsentscheidung beteiligt war, als eigene Ungleichung definiert werden, welche das Entscheidungsproblem abbildet. Dies resultiert in über 1000 Attributen, welche ein Objekt auf dem Förderband in seinen charakteristischen Ausprägungen widerspiegelt. Allerdings kann hierfür keine statische Pose des Menschen auf dem Förderband angenommen werden, da ansonsten nur diese eine Pose zur Erkennung des Menschen führt, was in einer sicherheitskritischen Anwendung nicht akzeptabel ist. Anschließend wird mithilfe von Marabou überprüft, ob diese Ungleichungen im Netzwerk widergespiegelt werden und das Neuronale Netzwerk somit mathematisch sicher die richtige Entscheidung trifft. Durch eine Kombination des Ansatzes mit Methoden der Explainable AI (xAI) konnten die Attribute aus den Laserscanner-Daten schlussendlich extrahiert werden, gegen welche anschließend getestet wird. Dabei zeigte sich, dass eine extreme Rechenleistung notwendig ist, um einzelne Laserstrahlen des vereinfachten Netzwerks zu überprüfen. Eine Überprüfung des gesamten Netzwerks würde voraussichtlich 75 Tage dauern. Eine Analyse der überprüften Ungleichungen hat ergeben, dass ca. 60% aller extrahierten Attribute im Netzwerk erkannt werden. Die restlichen Attribute konnten in dem Netzwerk nicht identifiziert werden. Je mehr Laserscanner bei der Betrachtung hinzugezogen wurden, umso weniger Attribute konnten im Netzwerk nachgewiesen werden. Ein Netzwerk grenzt seine Entscheidung also nicht klar ab, sondern besitzt eine weiche Entscheidungsgrenze, die mit Unsicherheit behaftet sein kann.

Die erzeugten Evidenzen waren für eine Beweisführung in einem Assurance Case leider nicht ausreichend, da nicht nachgewiesen werden kann, weshalb mehr als die Hälfte der Ungleichungen als »unsicher« eingestuft wird. Dies würde weitere Untersuchungen erfordern, die den Rahmen des Exploring Projects weit überschreiten. Deshalb wird, in Absprache mit der University of York, für den Assurance Case eine andere Beweisführung angestrebt. Hierbei soll die statistische Validierung im Vordergrund stehen. Die Evaluierung von formalen Methoden im Bereich des Maschinellen Lernens hat ergeben, dass die Extraktion von Attributen für ein Entscheidungsproblem eine komplexe Aufgabe ist, da die Charakteristiken eines Objekts in eine mathematische Repräsentation überführt werden müssen. Ebenfalls ist die mathematisch korrekte Überprüfung eines Neuronalen Netzes rechenintensiv und langwierig, welches die Anwendung in realitätsnahen Applikationen hemmt.